Abordarás el estudio y problemática sobre la importancia y utilidad de los límites y continuidad en escenarios empresariales y que además forman parte de la vida diaria de cualquier profesionista, por ello, es importante que tu aprendizaje sea significativo.
En el presente tema estudiarás el concepto de límite y cómo describe de forma precisa el comportamiento de una función cuando los valores de la variable independiente están muy próximos, aunque nunca igual, a un valor constante y su utilidad en los procesos económico-administrativos, tales como rendimiento y producción máxima; asimismo, determinarás cuando una función es continua y su aplicación en procesos productivos y su impacto en los costos de producción.
Problemática
Resulta fundamental conocer lo que aporta una unidad adicional vendida o producida a las funciones de ingresos, costos y utilidades en una empresa, para determinar la eficiencia y eficacia en su operación. Para ello se debe utilizar el cálculo diferencial, cuyas bases se originan en la obtención de los límites y la continuidad de una función.
De no conocer lo anterior las empresas pueden no maximizar sus utilidades, ni minimizar sus costos, en consecuencia, podría llevarlas a comenzar a perder utilidades, participación de mercado, clientes e incluso cerrar.
Con el álgebra de límites te puedes aproximar a un valor, ya sea un número cualquiera o el infinito, de manera exacta. Así, se puede decir que el límite de una función describe el comportamiento de una función f(x) conforme la variable independiente se aproxima a un valor constante.
Ejemplo
Se tiene la función:
f(x)=3x²-1
x-1
Y se requiere determinar su comportamiento cuando los valores de "x" tienden o se acercan a 1.
Solución
Se puede observar que la función no está definida en x=1, esto es porque cuando "x" toma el valor de 1, la función tiende al infinito, ya que cualquier número dividido entre cero es igual a infinito.
Sin embargo, sí se puede determinar el comportamiento o valores que va tomando la función cuando x→1 (x tiende a 1), ya sea con valores más pequeños a uno o bien más grandes a uno: 1 > x > 1.
Como pudiste observar, conforme "x" se acerca a 1 la función es igual a ± 20000, dependiendo de si se va acercando por la derecha o por la izquierda, es decir:
En conclusión se tiene que:
Cuando f(x) se acerca cada vez más a un número Límite (C), conforme "x" se aproxima a un valor constante “a” por cualquier lado, entonces "C" será el límite de la función y se escribe:
lim f(x)= C
x→a
Operación para determinar los límites de una función
Desarrollo
En la presente fórmula de álgebra de límites se puede observar que para evaluar el límite de una función sea f(x), g(x) o cualquiera, se tiene que sustituir en dicha función el valor del número hacia el cual tiende "x" y el resultado será siempre un número constante:
limx→a f(x)= C
limx→a g(x)= D
En esta segunda fórmula se observa que para sumar o restar dos funciones evaluadas en el valor hacia el cual tiende "x", se puede obtener de manera independiente el resultado de cada función al sustituir el valor de "x" en cada una y finalmente sumar o restar ambos resultados según sea el caso.
lim[f(x) ±g(x)]=lim f(x)±lim g(x)=C±D
x→a x→a x→a
En el siguiente caso se tiene que para multiplicar dos funciones evaluadas en el valor hacia el cual tiende "x" se puede obtener de manera independiente el resultado de cada función al sustituir el valor de "x" en cada una y finalmente multiplicar ambos resultados.
lim[f(x) *g(x)]=lim f(x)*lim g(x)=C*D
x→a x→a x→a
En la siguiente fórmula se tiene que para dividir dos funciones evaluadas en el valor hacia el cual tiende "x", se puede obtener de manera independiente el resultado de cada función al sustituir el valor de "x" en cada una y finalmente dividir ambos resultados.
En esta fórmula el valor hacia el cual tiende "x" se sustituye en la función y posteriormente se evaluará la potencia a la que está elevada la función.
lim xⁿ= aⁿ
x→a
En esta última fórmula de igual manera sustituyes el valor de "x" en la función y posteriormente calculas la raíz "n" a la que está elevada "x".
lim ⁿ√x= ⁿ√a
x→a
Conclusión
El evaluar un límite de una función es tan simple como sustituir el valor hacia el cual tiende "x" en la función. Al aplicar el álgebra de límites, únicamente aplicas las operaciones de suma, resta, multiplicación, división, raíz n-sima y elevar a una potencia en los resultados obtenidos de las funciones a las que ya se les ha sustituido el valor límite.
Límites de una función y sus propiedades
Existen diferentes límites de una función, a continuación se te muestra el limite de función y su procedimiento.
Función constante
Si se tiene una función constante f(x) = C, el límite de la función cuando "x" tienda a un valor “a” será siempre "c", esto es:
limC=C
x→a
x→a
lim[f(x)=C]
x→a
Ejemplo
Para determinar el límite de la función: f(x)=10, cuando x→8. Y siguiendo el razonamiento de la fórmula general anterior, se tiene que:lim[f(x)=10]
x→8
lim10 = 10
lim10 = 10
x→8
Función idéntica
Si se considera la función idéntica f(x)=x cuando "x" tiende a un valor “a”, su límite será siempre el valor constante “a”, es decir:
lim[f(x)= x]
lim[f(x)= x]
x→a
lim x = a
lim x = a
x→a
Ejemplo
Para determinar el límite de la función: f(x)=x cuando x→3. Siguiendo el razonamiento de la fórmula general anterior, se tiene que:
lim[f(x)= x]
x→3
lim x = 3
lim x = 3
x→3
Límites infinitos
Cuando se tiene una función racional f(x)=p(x)/q(x) en la que q(x) se hace cero cuando "x" tiende a un valor constante “a”, entonces f(x)=∞, es decir:
Para determinar el límite de la función: f(x)= x+3/x²-1 cuando x → 1, sustituyendo el valor de "x" en la función, se tiene que:
Para cualquier función f(x) se tiene que el límite de la función cuando x → a es el número constante que resulta de sustituir el valor de “a” en la función.
Ejemplo 1
Para determinar el límite de la función: f(x) x³+3x-2 cuando x→0 y cuando x→5. Sustituyendo el valor de "x" en la función para cada caso se tiene que:
lim[f(x)= x³+3x-2]
x→0
lim[x³+3x-2]=(0³)+(3*0)-2=-2
x→0
lim[x³+3x-2]=(0³)+(3*0)-2=-2
x→0
lim[f(x)= x³+3x-2]
x→5
lim[x³+3x-2]=(5³)+(3*5)-2=138
x→5
lim[x³+3x-2]=(5³)+(3*5)-2=138
x→5
Ejemplo 2
Para determinar el límite de la función: f(x)=5x+3/2x²-1 cuando x → 0 y cuando x → 2. Sustituyendo el valor de x en la función se tiene que:Cuando x→∞
El valor de la función puede crecer o decrecer indefinidamente, sin embargo, existen casos en los que la función adquiere valores reales.
A continuación verás ejemplos para el cálculo de límite de una función cuando la variable independiente tiende al infinito.
¿Cuál será el límite de f(x) = 7x4 – 2x3 + x2 +100 cuando x →∞?
Solución: al aplicar el límite infinito en la función se tiene que:
lim[f(x)=7x⁴-2x³+x²+100]
x→∞
lim[f(x)=7x⁴-2x³+x²+100]=7∞⁴-2∞³+∞²+100=∞
x→∞
Nota: observa que el coeficiente con mayor potencia tendrá como resultado un valor infinito, al sustituir el límite de la función.
Ejemplo
En una fábrica de electrodomésticos se tienen costos fijos de producción de $1’000,000.00 anuales y sus costos específicos son del orden de $430.00 por electrodoméstico. ¿Hasta qué punto puede reducir los costos promedio de producción al aumentar la producción indefinidamente?Solución
Se observa que la función de costo tendrá la forma C(x)=430x + 1’000,000, en donde x representa la cantidad de electrodomésticos producidos, de ahí que para determinar el costo promedio de producción se tendrá que dividir la función de costo entre el número de artículos a producir (x):C(x)=430x+1’000,000
x x x
C(x)=430x + 1’000,000
x x
Y si lo que se desea conocer es el costo promedio de producción cuando el nivel de producción se eleve indefinidamente se tiene que:
Por lo tanto, el costo promedio de producción será de $430.00 cuando el nivel de fabricación de productos electrodomésticos crezca indefinidamente.
Nota: Es importante notar que cuando se divide un número cualquiera entre ∞ el resultado siempre será cero, ya que el valor del divisor siempre será mucho más grande que el valor del número que se quiere dividir.
Ejemplo
El nivel de satisfacción de clientes en un autoservicio, de acuerdo al número de artículos comprados, fue medido a través de la siguiente función:
5(x) = 250x²
3x²+0.25x-0.001
En donde "x" representa el número de artículos comprados.
¿Cuál será el nivel de satisfacción del cliente conforme aumentan sus compras?
¿Cuál será el nivel de satisfacción del cliente conforme aumentan sus compras?
Solución
Si se considera que el cliente comprará un número infinito de artículos se puede observar cuál será el comportamiento del nivel de satisfacción del cliente en el punto más alto de sus compras:
lim = [ 250x² ]
x→∞ 3x²+0.25x-0.001
Con el fin de eliminar la indeterminación, en el caso de una función racional es conveniente dividir cada uno de los factores de la función entre la variable independiente con la potencia más alta "x²", así se tiene que, para este caso en particular.
Por lo que el nivel de satisfacción del cliente será del 83.33% y nunca podrá ser mayor a éste.
Se pudo observar, al realizar el cálculo de límites de una función, no siempre el límite coincide con el valor de la función en el punto hacia el cual se aproxima la variable independiente, esto es fácil de detectar al graficar la función en los valores cercanos al límite, ya que la gráfica de la función se puede cortar o tener una interrupción en algún punto cercano al límite.
Por ejemplo, se tiene la siguiente función:
f(x)=3x²-1
Por lo que el nivel de satisfacción del cliente será del 83.33% y nunca podrá ser mayor a éste.
Diferencia entre las funciones continuas y discontinuas
Funciones continuas
Son aquellas cuyas gráficas se pueden dibujar en un sólo trazo, es decir, si no presentan cortes o puntos de discontinuidad.Funciones discontinuas
Es discontinua si hay puntos en los cuales existe una pequeña variación de la variable independiente, lo que genera un salto en los valores de la variable dependiente.Se pudo observar, al realizar el cálculo de límites de una función, no siempre el límite coincide con el valor de la función en el punto hacia el cual se aproxima la variable independiente, esto es fácil de detectar al graficar la función en los valores cercanos al límite, ya que la gráfica de la función se puede cortar o tener una interrupción en algún punto cercano al límite.
Por ejemplo, se tiene la siguiente función:
f(x)=3x²-1
x-1
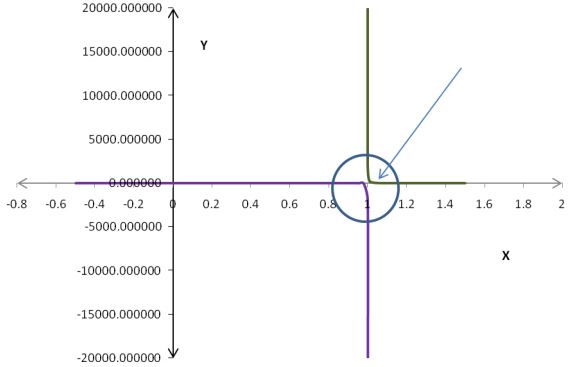
en la que se dice que x → 1, y que al graficar las coordenadas que van acercándose al límite se tiene la siguiente gráfica:
En donde se observa que hay un punto exactamente cuando x = 1 en el que la gráfica de la línea ya no continúa con el resto de los valores, es decir, que hay una ruptura en la gráfica.
De ahí que se puede definir que una función es continua cuando no se presenta un corte en la línea que representa su gráfica, mientras que en una función discontinua se presentan cortes en la línea que representa la gráfica de la función.
Así se tienen tres condiciones que permiten descubrir si una función es continua o discontinua:
➊ Una función será continua si f(x) está definida en x=a, es decir, que sus valores son reales.
➋ Una función será continua si el Límite de la función f(x) cuando x→a existe.
➌ Una función será continua si: lim x→a f(x)=f(a)
Por lo que si una de las condiciones anteriores no se cumple, la función será discontinua.
Operaciones con funciones continuas
Si las funciones f(x) y g(x) son continuas en un punto a, entonces las funciones podrán sumarse, multiplicarse o dividirse (para g(x) ≠ 0 en el caso de división).
Toda función polinomial es continua.
El modelo gráfico que representa a esta función de oferta vs demanda es:
Ejemplo
Oferta y demanda
Un vendedor de aceites orgánicos en frascos de 250 ml vende aceite de uva a $90.00 cada frasco, pero si le compran más de 10 frascos el precio por frasco es de $85.00.
¿Qué se le podría recomendar al vendedor para que pueda conservar su escala de precios de mayoreo sin que se le presenten problemas económicos con su promoción?
Con lo que se observa que el precio de 10 frascos es de $900.00 y de 11 frascos es de $935.00, por lo que para evitar contradicciones, el precio de 11 frascos debe ser superior al de 10; si se dice que "p" es el precio de cada frasco de aceite cuando se compran más de 10 frascos, se debe cumplir que 11p > 900, es decir, p > 900/11 = $81.81, por lo tanto, el vendedor debe asignar un precio superior a $81.81 para cada frasco cuando le compren más de 10 frascos de aceite de uva.
En esta unidad estudiaste el concepto de límite y cómo describe de forma precisa el comportamiento de una función cuando los valores de la variable independiente están muy próximos a un valor constante. Es de gran utilidad en los procesos económico-administrativos, tales como rendimiento y producción máxima.
Pudiste observar cuando una función es continua, su aplicación en procesos productivos y su impacto en los costos de producción.
La solución de problemas de límites y continuidad de una función te permitirán determinar su impacto en los procesos económico-administrativos, como pudiste observar en los ejemplos que se te proporcionaron.
Recursos de apoyo
Universidad Técnica Particular de Loja
Definición de límite
Discontinuidad de una función
Análisis Matemático - EducatinaFunción continua o discontinua con límites (continuidad de funciones)
Ejercicios
Bibliografía básica
►Chiang. (2006). Métodos fundamentales en economía matemática. (4° edición). Editorial México: McGraw-Hill.►Harshbarger, R. J. & Reynolds, J. J. (2005). Matemáticas Aplicadas a la Administración, Economía y Ciencias Sociales (7° edición). México: McGraw-Hill.
►Leithold, L. (2006). El cálculo. (7ª edición). Oxford: Editorial Cúspide.
►Render, B., Stair, R., Hanna, M. (2006). Métodos cuantitativos para los negocios. México: Pearson Educación.
►Thomas. (2006). Cálculo de una Variable. Editorial Prentice Hall.
Bibliografía complementaria
►Cissell, R., Cissell, H. y Flaspohler, D. (1999). Matemáticas Financieras. (2ª edición). México: Editorial CECSA.►García, E. (1998). Matemáticas Financieras por medio de Algoritmos, Calculadora Financiera y PC. México: Editorial McGraw-Hill.
►Hernández, A. (1998). Matemáticas Financieras Teoría y Práctica. (4ª edición). México: Ediciones Contables, Administrativas y Fiscales.
►Motoyuki, A. (2000). Matemáticas Financieras. Córdoba, Argentina: Despeignes Editora.
►Spiegel, M. R. (1994). Manual de Fórmulas y Tablas Matemáticas. Traducción de la 1° edición. México: McGraw-Hill.
►Toledano y Castillo, M. A. y Himmelstine de Chavarria, L. E. (1984). Matemáticas Financieras. México: Editorial CECSA.
►Vidaurri, H. M. (2001). Matemáticas Financieras. (2ª edición). México: Ediciones Contables, Administrativas y Fiscales - Thomposn Learning.










0 comentarios:
Publicar un comentario