La división sintética es otra alternativa metodológica para la resolución de divisiones, para explicar los pasos para la resolución de divisiones por medio de la regla de Ruffini tomaremos como ejemplo la división: x⁴-3x²+2÷x-3
Paso 1
Ordenar según su potencia de mayor a menor. Si el polinomio no está completo lo completaremos añadiendo los términos que faltan con ceros.
Paso 2
Colocamos los coheficientes del dividendo en una línea.
Paso 3
Abajo, a la izquierda colocamos el opuesto del término independiente del divisor.
Paso 4
Trazamos una raya y bajamos el primer coheficiente
10-302
3 .
1
Paso 5
Multiplicamos ese coheficiente por el divisor y lo colocamos debajo del siguiente término.
10-302
3 3 .
1
Paso 6
Sumamos sus dos coheficientes
10-302
3 3 .
13
Paso 7
Repetimos el proceso anterior.
10-302
3 3 91854.
13618|56
Paso 8
El último número obtenido es 56 que es el resto.
Sin embargo no siempre se puede utilizar la división sintética en los polinomios, ya que el divisor tiene que ser forzosamente de grado uno d(x)=x±a.
Comprobación:
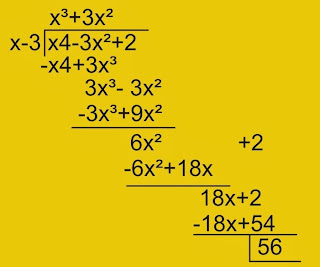
0 comentarios:
Publicar un comentario